先日、ある方からこんな相談を受けました。
うちの子は、小学校から学習塾に通い、それなりの成績を維持してきましたが、高校に入ってから途端に成績が下がってしまいました。理系科目が得意だったので、理系に進みましたが、数学・物理がとても苦しい状態になってしまいました。何が原因なのでしょう。
この様な相談は、意外と多いので、なぜ、高校で大変なことになってしまうのか、どう対応すればいいのか整理しておきます。
- 机上の学習をメインにし、暗記で何とか問題を解こうとしてきたため。
- 模試などの結果だけを重視した暗記型の指導が行われることが多いため。
つまり、
できるだけ暗記する要素を減らす努力をする必要がある。
具体的にどういうことか、簡単な事例を挙げながら解説し、最後にどの様にすれば、いいのか改善策を紹介します。
【要注意】公式を暗記して勉強してきた子は、高校でつまずきやすい!

小中学生で「数学や理科は公式を覚えるだけで問題が解けるから簡単!」という人に出会うことがありますが、こういった子どもは、残念ながら高校でつまずいてしまう可能性がかなり高いです。
極めて簡単な例を一つ挙げるとすると、
台形の面積=(上底+下底)×高さ÷2
なぜ、この様な式になるのか、説明できない場合、いくら小中学校のテストの結果が良くても、勉強の仕方が間違っていると判断していいでしょう。
この説明は、とても簡単なことですが、「分からない」という中学生もたくさんいるのが現状です。
【高校物理から簡単な事例】丸暗記で困ってしまった事例
高校物理で取り扱う公式は、山盛りあります。どの公式を1つとしてカウントするか、難しいところですが、100種類くらいはあるかと思います。
実は、今回相談のあった高校生は、学校で「とりあえず公式を覚えたら問題は解ける」と先生に言われたことを鵜呑みにして、公式を覚えて、あてはめて答えを導くという学習をしてきた様です。
その結果どうだったか…
- 最初は、学習範囲も狭く、難易度も低いために公式を暗記するスタイルでも順調。
- 学習が進み、利用する公式も増え、難易度が高くなるとどの場面でどの公式を使ったらいいのか分からない。
こんな風になってしまい、単位取得も危ないと学校から言われてしまったということです。次の様な基本的な問題にも困ってしまうという状況でした。
2.0×105 Paで5.0Lの気体を2.5Lにすると圧力は何Paになりますか。
ただし、温度は一定のままとする。
ボイルの法則(P1V1=P2V2)より、
2.0×105 ×5.0=P2×2.5
P2=2.0×105 ×5.0÷2.5=4.0…×105 答え4.0×105Pa
こんなものを見せられると、物理が嫌いになる人がほとんどじゃないかなぁと思います。ところが、この問題、ボイルの法則を知らない小学生でも感覚的には解くことができます。
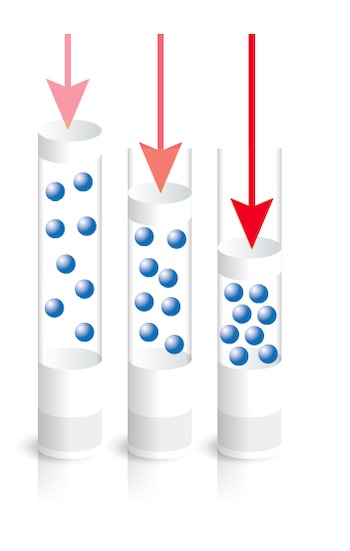
左の図の様なイメージで考えると、体積が0.5倍(2.5÷5.0)になっているので、圧力は、最初の圧力より2.0倍になると考えることができる。
だから、
2.0×105 2.0=4.0×105となると思う。
つまり、生活の中から上の図の様な体験(空気鉄砲や注射器遊びなど)をイメージすることができれば、ボイルの法則が成り立つことも理解することができるということです。
ここで取り上げたものは、とても簡単な例ですが、この様な簡単な例でさえもイメージせずに勉強をしている高校生は案外多いものです。何もイメージせずに勉強をすると、最初の解答例に挙げたただの計算処理に終わってしまい、面白さを感じることもできなくなってしまいます。
【高校数学の三角関数の公式】本当にそうなのか疑うことが大切
物理の公式を丸暗記で何とかしのいできた彼の場合は、数学の三角関数の公式も丸暗記作戦で何とかしようと思っていたようです。一つの考え方が様々なところに影響を及ぼす一つの事例です。
本当にそうなの?と疑う大切さと、考え方の簡単な事例を一つ紹介します。
Sin2θ+Cos2θ=1
よく「これくらいは覚えておこう」と言われる公式ですが、なぜ、Sin2θ+Cos2θ=1が成り立つのか考えて見ることは大切です。Sinθ・Cosθの定義は理解しておく必要がありますが、それさえ分かってしまえば、中学生でも十分、説明することができます。
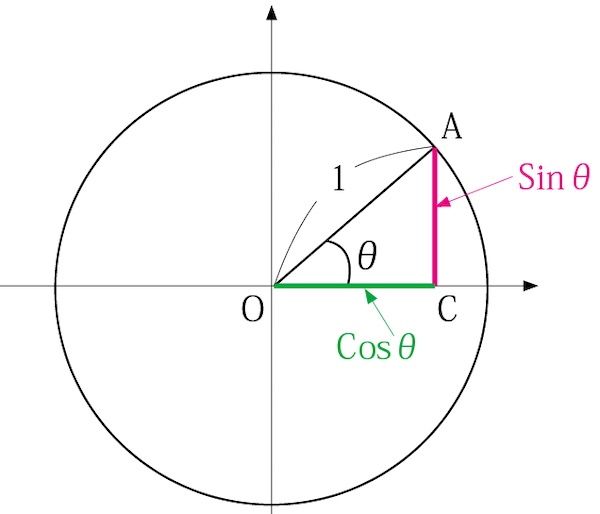
半径を1とする円の中に、左の図の様な三角形AOCを描く。
Sinθの定義よりAC=Sinθ
Cosθの定義よりOC=Cosθ
三角形AOCは直角三角形なので、平方根の定理を使うと、
Sin2θ+Cos2θ=1が成り立つ。
一手間かかりますが、本当かどうかを自分で確かめることは、大切です。実は、そういう習慣を身につけるためにも勉強をしているのです。
これがどういうことか、詳しく解説します。
なぜ、そうなるのかを考える習慣をつけるための練習が勉強

高校生の勉強はなかなかハードなので、
こんな勉強をして何の意味があるの?生活で使うことなんてない!
と思うこともたくさんあって当然ですが、大切なのは、「〇〇となる」と言われたことを…
- 本当にそうなのか、自分で考えてみる。
- なぜ、その様な結果になるのか考えてみる。
このような思考方法を勉強を通して行っているのです。
この考え方がとても大切だということは、近年で言えば「コロナワクチンの接種」とも深い関係があります。国や行政・医師が「ワクチン接種で重症化のリスクが抑えられる」と盛んに言っていましたが、ここで、「本当かなぁ?」とまず自分で考えてみることが大切だということです。
こうしたことを話すと、「医療の専門的な知識がないから…」と言われる方もいらっしゃいますが、
- ワクチンの歴史を調べてみる。
- 遺伝子の基本的な性質を調べてみる。
この様なことは、凡人の私でもすることができます。そうすると、
- テレビや新聞がワクチンを推奨していたから、接種することにした。
- 有名なお医者さんが、ワクチン接種を推奨していたから、接種することにした。
という理由よりも確かな根拠がもてるようになるはずです。
実は、コロナワクチンの接種に関する決断理由を様々な人に聞いてきましたが、「〇〇(メディア・行政・医師など)が接種した方が良いと言っていたから」という声が、かなり多かったのです。
まさに「教科書に公式が書いてあったから」「〇〇になると覚えておいたら良い」という発想が大人社会にも見事に反映されていると感じた出来事でした。別の見方をすると、自分なりの方法で確かめてみようとする人が少ない社会を教育によって作ってきたとも言えるのです。
長く教育に関わっているものとして、たくさんの事を考えさせられる出来事だったのです。
最後までお読みいただきありがとうございます。
庭に植えているネギの様子を見ながら、なぜ、ネギはあんなスリムな葉にしているのだろう?光合成をしっかりしたいのであれば、大きな葉をつけたらいいのに…なんて考えています。











コメント