小学校の算数で「割合」は、なかなか難しい単元とよく言われます。
が、割合を難しくしているのは、なぞの公式「くもわ」の存在です。
私の場合、これまでに200人以上の子ども達に「割合」の学習を指導してきましたが、
- 「くもわ」は一切教えていません。
- 教科書に書かれている公式も教えたことがありません。
それでも、ほぼ100%の子どもが割合を理解することができています。
今回は、どの様にして割合を指導してきたのか、詳しく解説します。
小学生が、「くもわ」などの存在によって「割合」の学習が難しいと感じる理由は、小学生が「割合」を難しいと感じる理由【公式を暗記するから】の記事で詳しく紹介しています。

小学校5年生の「割合」の学習は、小学校3年生で概ね学習済み!

割合の限らず、算数・数学でつまずいている子どもの多くは、
- 答えさえ求めることができたらいい(テストで点数がとれたら良い)。
- とにかくやり方を暗記して、情報を処理すれば良い。
と思っている子どもがほとんどです。
これでは、少しひねった問題に到底対応することができません。
それ以上に、「解き方を創造する」という楽しさを味わうことができないために、勉強の楽しさを感じにくくなってしまうというのが、大きな問題です。

私は、長年「くもわ」で指導をしてきたけれども、それ以上にいい方法ってどんな方法なんだ?
割合とは?定義を確認してみよう
東京書籍の教科書には、次の様に書かれています。
もとにする量を1と見たとき、比べられる量がどれだけにあたるかを表した数を割合と言います。
(東京書籍 新しい算数下より引用)
なかなか難しい表現ですが、この話を簡単に表現すると、
ということになります。なぜ、そう言えるのか、解説します。

お姉ちゃんのお小遣いは、私の2倍もあるの。
っていうのも割合の話をしたってことになるの?
割合=何倍かを表した数と言える具体例
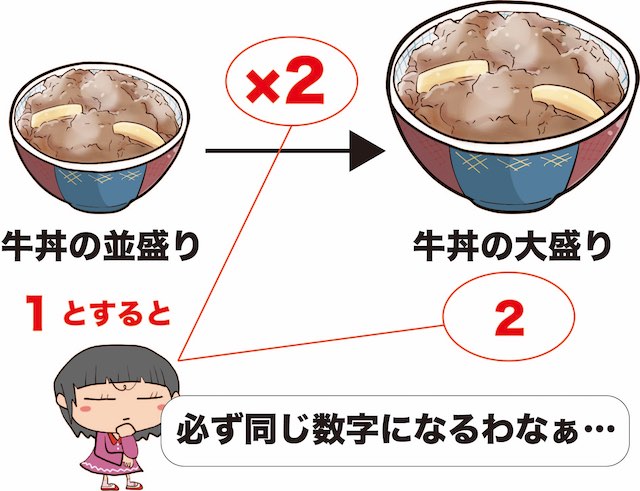
この時、上の図の様に「並盛りの牛丼の量」を1とすると、「大盛りの牛丼の量」は2となります。
この話を教科書の定義に当てはめると、
- もとにする量=牛丼の並盛りの量=1
- 比べられる量=牛丼の大盛りの量=2
となりますが、こんな難しいことを考えなくても、下の図の通り、もとにする量は必ず1なので、何倍か表した数=比べられる量になります。
ということで、私が割合の指導をする際には、教科書と表現は異なりますが、割合=何倍かを表した数という定義で学習をすすめています。
割合を学習していなくても、割合を求めることができる!
簡単な例題を挙げてみましょう。
数字が簡単なので、
1000÷500=2 答え2倍
と即答できるはずです。
この「2」という数は、詳しく見ると、はなちゃんのお小遣いを1とした時に、お姉ちゃんのお小遣いは2ということですから、実は、すでに割合を求めたということになるのです。
ここで重要なのは、2を求めるのに公式を使う子はいないということです。
上記の問題を「割合」という言葉を使って書き直すと次の通りになります。
こんな表現になってしまいますが、要するに、お姉ちゃんのお小遣いは、はなちゃんの何倍かを聞かれていることが分かれば、全く問題ありません。
【具体例】割合の定義が分かれば、くもわも公式も必要ない!

繰り返しになりますが、
ということで、実際の問題を解いてみましょう。
「くもわ」や公式は必要ないことが感じられるはずです。
割合=何倍かを表した数なので、この問題は、次の様な意味になります。
これを関係図に整理すると…

ここまで整理することができれば、
24×?=6
6÷24=0.25
答え 0.25(倍)
と答えを求めることができます。
【補足】問題文から関係図に表すのが難しいと思った場合
上記の問題から関係図に表すのが難しいと感じた方は、数字を置き換えた次の問題で考えてみましょう。
現実にはあり得ないことですが、分かりやすくするために次の様に問題文を変更しました。

48÷24=2
答え 2(倍)
と求めることができます。
もちろん、ここでも公式や「くもわ」を意識する必要はありませんでした。
割合は2つの量の比較なので基本は3種類の問題しかない!

基本的な割合の問題は3種類しかない
算数で学習する割合は、基本的に上記の3種類を求める問題しかありません。
発展的な内容のものも、以下に紹介する3種類の考え方の組み合わせによるものです。
なお、この3種類を見ても、公式は覚える必要はないことが分かります。
割合(何倍か)を求める問題
本記事で既に紹介しました。

関係図の真ん中が分からない形でです。
を求めればよいことが分かります。
比べられる量を求める問題

関係図にすると右側が分からない形の問題です。
を求めればよいことが分かります。
もとにする量を求める問題
お姉ちゃんは毎月1000円もらっていて、これは、はなちゃんのお小遣いの2倍だそうです。はなちゃんは、毎月何円のお小遣いをもらっていますか。
関係図にすると左側が分からない形の問題です。
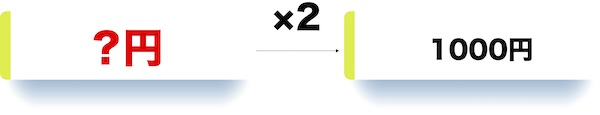
を求めれば良いことが分かります。
いずれも、関係図(〇〇は□□の何倍という関係を表す図)に整理さえすれば、どの様に計算すればいいのかは、見えてきます。
「公式を覚えて使う」学習から「公式を作る学習」に

理系で様々なことを学んだ方は、
という認識の方が強いでしょう。
ところが、世間一般的には、まだまだ「公式を覚えるもの」という認識が強いのが現状です。
もちろん、覚えることは悪ではありませんが、
だという理解をしておきたいです。
早く結果を出すには、暗記をしてしまえばいいのですが、学習レベルが高くなるほど、創造性が求められます。
何より、公式に限らず、自分で本当かどうかを確かめたことは、忘れる可能性がかなり低くなり、一つの真実として自分の糧となってくれるのです。
このことを私たち大人は子どもに伝えなければいけません。
本日も最後までお読みいただきありがとうございます。
先日も、これまで暗記で乗り越えてきた中学生の学習の様子を見ましたが、問題のスタイルが少し変わると、全く解けないという状態でした。
日々、厳しい学習塾で、驚くほどの量の問題を解いているにも関わらず、彼女は困ってしまっていたのです。
指導者は何に力点をおいて教えるべきか、今一度、考える必要がある様に思います。






コメント