算数・数学を勉強していると、様々なところで、「次のようなことが成り立ちます」と書かれた文に出会います。
先日は、小学生の子ども達と、小数の分配法則・結合法則について学習をしていました。
(a−b)×c=a×c-b×c
整数の場合と同様に小数の場合にも、この様な性質が成り立ちます。
この様に、書かれていますが、鋭い小学生からは次の様な質問をされました。

整数の場合、成り立つのは分かるけれども、本当に小数の場合でも成り立つの?確かめないといけないじゃん。
大人の私たちからすれば、「そりゃそうでしょ」という感覚かもしれませんが、本当かどうかを確かめることは、とても大切です。
そこで、次の様な方法で確かめました。
小数でも分配法則・結合法則は本当に成り立つのか?

分配法則・結合法則には、足し算の場合・引き算の場合がありますから、それぞれ次の様な問題を解きながら確認しました。
この時に使った問題は、無料の学習プリントのページに掲載しています。
【足し算の場合】小数の分配法則・結合法則を確かめる問題
次の様な問題を解くことで、分配法則・結合法則を解くことができます。
整数と小数が混じった問題
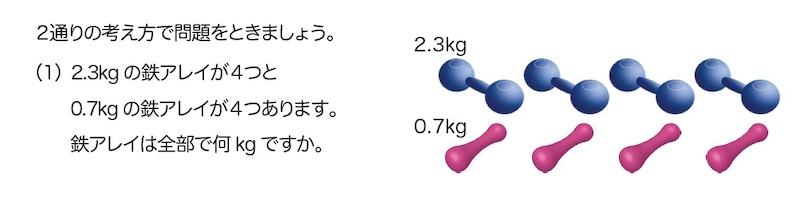
小数と整数が混じっても分配法則・結合法則は成り立つかを確かめる問題
考え方①
問題を素直に読み、立式すると、次の様な考え方になります。
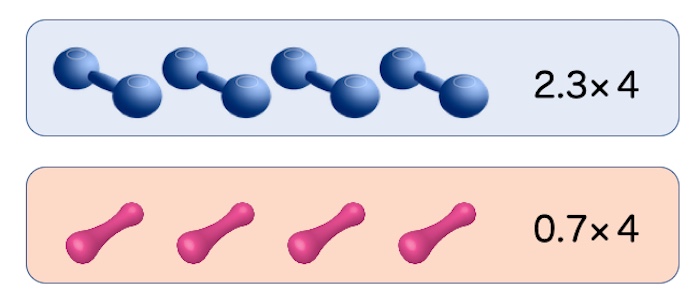
小数と整数が混じっても分配法則は成り立つか確認する問題
式の形で整理すると、
となります。
考え方②
2.3kgと0.7kgをセットにして考える方法で、次の様になります。
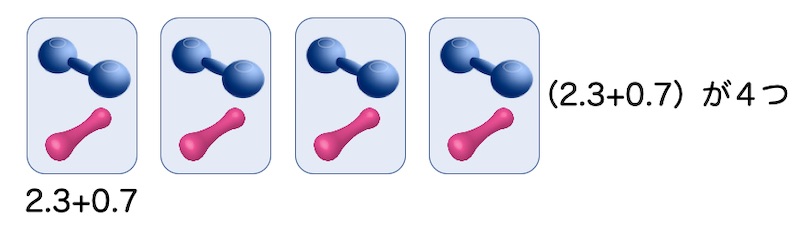
小数と整数が混じっても分配法則は成り立つか確認する問題
式の形で整理すると、
ということになり、整数と小数が混じった場合でも、分配法則・結合法則は成り立つと言えそうです。

じゃあ、全部が小数の場合はどうなるの?
【引き算の場合】小数の分配法則・結合法則を確かめる問題
では、次に、
- 引き算の場合でも分配法則・結合法則は成り立つのか?
- 全ての数値が小数でも分配法則・結合法則は成り立つのか?
について考えてみましょう。
そこで、次の様な問題を準備しました。
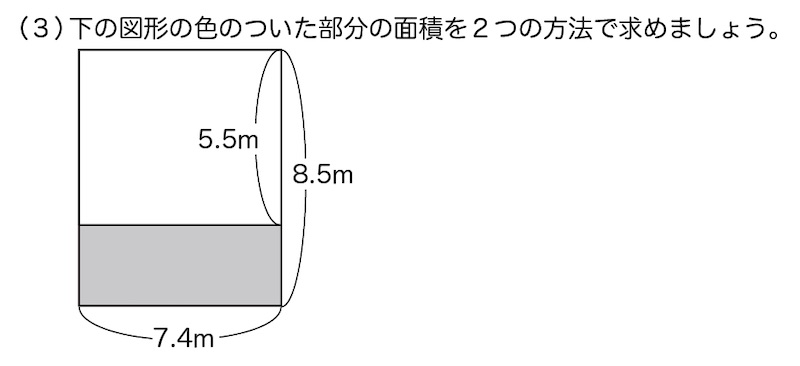
引き算でも分配法則・結合法則は成り立つのか?を確かめる問題
2つの方法で色のついた部分の面積を求める方法を考えます。
考え方①
面積は、縦の長さと横の長さが分かれば求められるので、次の様な考え方ができます。
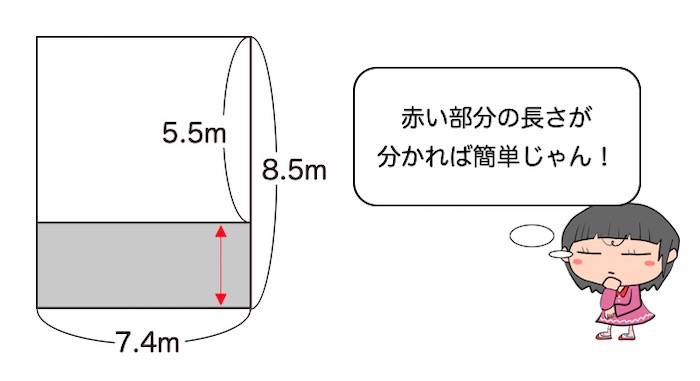
引き算でも分配法則・結合法則は成り立つのか?を確かめる問題
式に整理すると次の様になります。
考え方②
また、四角形全体から不要な部分(白い部分)を切り取るイメージで計算をしても、色のついた部分の面積を求めることができます。
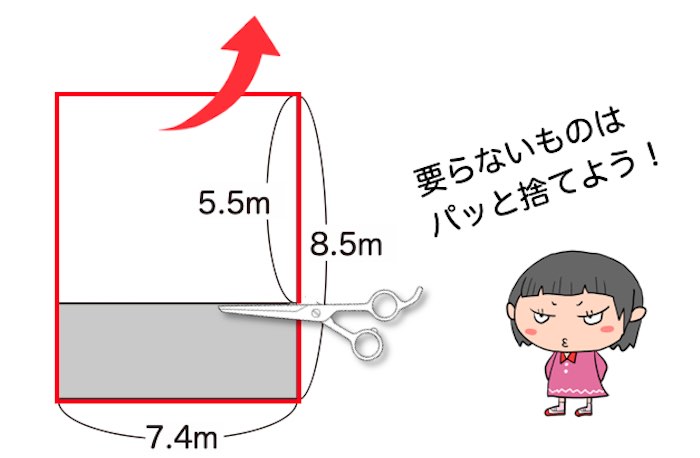
引き算でも分配法則・結合法則は成り立つのか?を確かめる問題
これを式に整理すると、
①=②となるために、全てが小数であっても、引き算が含まれる場合であっても、分配法則・結合法則は成り立つことが分かります。
深く学ぶということとは?

様々な保護者、そして塾や学校の指導者と接していると、テストの結果をとても重視されていると感じることがあります。
もちろん、子ども達の将来を考え、結果を意識することも大切ですが、本当の学びというのは、
- 不思議だと感じること。
- 不思議だと感じたことについて試したり、その理由を追求すること。
だと思います。これを一言で言うなら、
だということです。
例えば、今回のケースで言えば、小数でも本当に分配法則・結合法則が成り立つのか?という質問でしたが、これを確かめたところで、テストの点数が上がることはありません。
そもそも、そんな問題を出題する先生は非常に少ないですから。
では、今回の様に「本当に成り立つの?」と考えたり、事例を挙げてみたことは無駄だったのでしょうか。
私はこの「本当なの?」と考えてみることが、学ぶことも面白さにつながると思うのです。
その証拠に、実際に生活をしていると、高校・大学・社会人…と成長するに連れて、「なんで?」と思うことはどんどん増え、ふとした瞬間に「あっ!そうだったのか。」と感じることはとても面白いと感じるからです。
何でも、「そういうもの」で済ませるのは簡単ですが、「なんで?」を考えるところに面白さが詰まっていると思うのです。
【小・中学生向】勉強が好きになる習慣を手に入れる3つの方法の記事も参考にしていただけると思います。

本日も最後までお読みいただきありがとうございます。
なぜ、昔はマイバック・マイ籠をもってスーパーに買い物に行く人が多かったのに、その習慣がなくなってしまったのだろう。
レジ袋が有料化になる時にこんなことを感じたものです。
そして、マイバックをもって買い物に行ってみて、その謎が解けました。
ボーッとしていたら、商品を手にとってマイバッグに入れそうになっていたのです。
危ない…危ない…。








コメント